¿Qué es la propiedad distributiva?
La propiedad distributiva es un principio matemático fundamental que permite reestructurar expresiones algebraicas. Se aplica sobre todo en la multiplicación y la suma, facilitando la realización de cálculos algebraicos. Este principio establece que el producto de un número y una suma es igual a la suma de los productos de ese número con cada uno de los sumandos.
Fórmula de la propiedad distributiva
Matemáticamente, la propiedad distributiva se puede expresar de la siguiente manera:
a(b + c) = ab + ac
En esta expresión:
- a es el multiplicando.
- b y c son los sumandos.
- ab y ac son los productos de a con cada uno de los sumandos.
Ejemplo básico de la propiedad distributiva
Para ilustrar mejor la propiedad distributiva, consideremos el siguiente ejemplo:
Si tenemos la expresión 3(4 + 5), podemos aplicar la propiedad distributiva para resolverla:
3(4 + 5) = 3 4 + 3 5
Calculando, obtenemos:
3(4) + 3(5) = 12 + 15 = 27
Por lo tanto, 3(4 + 5) = 27, lo que confirma que la propiedad distributiva se ha aplicado correctamente.
Propiedad distributiva con números negativos
La propiedad distributiva también se aplica a los números negativos. Por ejemplo, consideremos la expresión:
-2(3 – 4)
Aplicando la propiedad:
-2(3) + -2(-4)
Esto se traduce en:
-6 + 8 = 2
Así, -2(3 – 4) = 2, mostrando que el principio es válido incluso con valores negativos.
Ejemplo con variables
La propiedad distributiva no se limita solo a números; también se puede aplicar a variables. Suponiendo la expresión:
x(y + z)
Aplicamos la propiedad distributiva:
xy + xz
Esto implica que si tenemos x = 2, y = 3, y z = 4, podemos evaluar la expresión original:
2(3 + 4) = 2 3 + 2 4
Calculando:
14 = 6 + 8
Aplicaciones de la propiedad distributiva
La propiedad distributiva es de gran utilidad en diversas áreas matemáticas, entre las que se incluyen:
Simplificación de expresiones algebraicas
Permite simplificar expresiones complejas. Por ejemplo:
5(x + 2) − 3(x + 3)
Usando la propiedad distributiva, se puede reescribir como:
5x + 10 – 3x – 9
Y simplificando:
2x + 1
Resolución de ecuaciones
Es útil al resolver ecuaciones. Tomemos la ecuación:
2(x + 4) = 24
Aplicamos la propiedad distributiva:
2x + 8 = 24
Resolviendo, tenemos:
2x = 16 → x = 8
Cálculos en álgebra avanzada
Además, en álgebra avanzada, la propiedad distributiva juega un papel crucial en la expansión de polinomios.
Por ejemplo, al expandir (x + 3)(x + 2):
x^2 + 2x + 3x + 6 = x^2 + 5x + 6
Propiedad distributiva en el contexto de las identidades algebraicas
La propiedad distributiva también se encuentra en diversas identidades algebraicas. Las más significativas son:
Identidad binómica
La propiedad distributiva se encuentra en la expansión de las identidades binómicas, como:
(a + b)² = a² + 2ab + b²
Aplicando la propiedad distributiva, se obtiene la expansión adecuada.
Productos notables
Los productos notables, como el cuadrado de una diferencia, se derivan de la propiedad distributiva, como:
(a – b)² = a² – 2ab + b²
Esto se puede verificar mediante la aplicación directa de la propiedad.
Para recordar la propiedad distributiva, es útil seguir algunos consejos prácticos:
Practica con ejemplos variados
Realiza ejercicios que incluyan tanto números positivos como negativos, y variables.
Visualiza la propiedad
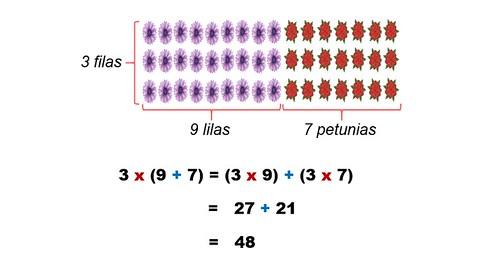
Dibuja diagramas o utiliza modelos visuales que representen los productos y las sumas. Esto facilita la comprensión del concepto.
Usa material didáctico
Utiliza aplicaciones educativas, juegos y recursos en línea que refuercen la práctica de la propiedad distributiva.
Errores comunes al aplicar la propiedad distributiva
Al aplicar la propiedad distributiva, es fácil cometer errores. Algunos de los más comunes son:
Es crucial aplicar la propiedad a cada sumando. Por ejemplo, en 3(x + 1 + 2), debe ser 3x + 3 1 + 3 2.
No prestar atención a los signos
Especialmente con números negativos, un descuido con los signos puede llevar a errores. Asegúrate de realizar cada multiplicación correctamente.
No simplificar correctamente
Después de aplicar la propiedad, no olvides simplificar los términos resultantes. La simplificación es una parte vital del proceso.
Ejercicios prácticos para reforzar la propiedad distributiva
Para poner a prueba tu comprensión de la propiedad distributiva, aquí algunos ejercicios prácticos:
- 4(5 + 6)
- 6(x - 3)
- 2(a + b + c)
- -3(2x + 5)
Resuelve estos ejercicios aplicando la propiedad distributiva y verifica tus resultados.
se puede afirmar que la propiedad distributiva es un pilar fundamental en el estudio de las matemáticas. Su comprensión y correcta aplicación son imprescindibles para avanzar en el álgebra y en niveles más complejos de la matemática. A través de la práctica y la atención a los detalles, cualquier estudiante puede dominar este concepto esencial.