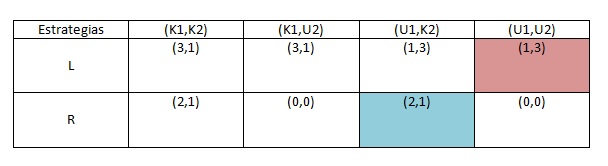
El equilibrio de Nash es un concepto fundamental en la teoría de juegos, desarrollado por el matemático estadounidense John Nash en la década de 1950. Este concepto describe una situación en la que, dado un conjunto de estrategias elegidas por los jugadores, ningún jugador tiene la oportunidad de mejorar su resultado individual cambiando su estrategia, siempre que los demás jugadores mantengan sus estrategias constantes.
Fundamentos de la teoría de juegos
La teoría de juegos es un ámbito interdisciplinario que estudia la toma de decisiones en entornos donde los resultados dependen de las elecciones de múltiples agentes. Este campo abarca diversos escenarios, desde la economía hasta las ciencias políticas, la biología y la psicología. En este contexto, el equilibrio de Nash se convierte en la herramienta clave para analizar situaciones de conflicto y cooperación.
En términos matemáticos, un perfil de estrategias (s1, s2, …, sn) es un equilibrio de Nash si, para cada jugador i, su estrategia si es la mejor respuesta a las estrategias elegidas por los demás jugadores. Esto se expresa matemáticamente como:
u_i(s_i, s_{-i}) ≥ u_i(s_i', s_{-i})donde u_i es la función de utilidad del jugador i, s_{-i} representa las estrategias de todos los demás jugadores, y s_i’ una estrategia alternativa. Esta condición garantiza que, dado el comportamiento de los otros, nadie se beneficiará de cambiar unilateralmente su estrategia.
Ejemplos ilustrativos
El dilema del prisionero
Uno de los ejemplos más conocidos del equilibrio de Nash es el dilema del prisionero. En este escenario, dos delincuentes son arrestados y se les ofrece la oportunidad de delatarse mutuamente o permanecer en silencio. Las posibles estrategias y sus respectivos resultados son:
- Si ambos permanecen en silencio, cumplen una pena de 1 año.
- Si uno delata al otro mientras que el otro permanece en silencio, el delator queda en libertad y el otro recibe 3 años de prisión.
- Si ambos se delatan, cada uno cumple 2 años de prisión.
El equilibrio de Nash aquí se produce cuando ambos jugadores eligen delatarse, aunque esta estrategia no maximiza su beneficio conjunto. Se observa que, desde el punto de vista individual, no sería beneficioso cambiar de estrategia una vez que el otro ha tomado su decisión.
El juego de la gallina
Otro escenario clásico es el juego de la gallina, donde dos conductores se dirigen uno hacia el otro en sus automóviles. Ambos tienen dos opciones: continuar y chocar o desviarse. Si uno se desvía y el otro no, el que se desvía pierde, pero si ambos se desvían, ambos ganan. El equilibrio de Nash aquí se encuentra en los casos en que uno de los dos se desvía mientras que el otro avanza, resultando en un riesgo calculado para la supervivencia de ambos jugadores.
Economía
El equilibrio de Nash tiene implicaciones significativas en la teoría económica. Por ejemplo, en el análisis de mercados oligopólicos, donde las decisiones de precios de unas pocas empresas interdependen entre sí. En este tipo de escenarios, las empresas deben considerar las reacciones de sus competidores al fijar sus precios, convirtiendo a la estrategia de cada empresa en una parte integral del equilibrio de mercado.
Sociología
La teoría de juegos también se aplica en la sociología para entender la dinámica de grupos y sociedades. Por ejemplo, los comportamientos de cooperación y conflicto en comunidades pueden analizarse mediante el enfoque del equilibrio de Nash, lo que nos permite comprender cómo se forman las normas sociales y cómo se mantienen. Las decisiones de los individuos en función de las elecciones de los demás crean un patrón que puede dar lugar a un equilibrio en situaciones de cooperación o competencia.
Biología evolutiva
En la biología evolutiva, el equilibrio de Nash se utiliza para explicar ciertos comportamientos animales y estrategias de supervivencia. Los especialistas en biología han modelado interacciones entre especies y su evolución a través de la teoría de juegos. Por ejemplo, en la lucha por recursos limitados, los animales deben decidir entre competir agresivamente o cooperar, basándose en las acciones de sus competidores. En este contexto, los equilibrios pueden reflejar estrategias que han evolucionado para maximizar las posibilidades de reproducción de cada especie.
Limitaciones del equilibrio de Nash
A pesar de su utilidad en numerosos campos, el equilibrio de Nash enfrenta críticas y limitaciones. Una de las principales críticas es que no siempre resulta en resultados óptimos para el grupo. En muchos casos, los equilibrios de Nash pueden llevar a situaciones subóptimas donde todos los jugadores terminan en desventaja, conocido como efecto de paradoja de la cooperación.
Equilibrios múltiples
Otra limitación es la posibilidad de que existan múltiples equilibrios de Nash en un solo juego. Esto presenta un desafío adicional para los analizadores, ya que la determinación de cuál equilibrio se alcanzará puede depender de una serie de factores, incluidos históricos, culturales y contextuales. La elección entre equilibrios puede ser influenciada por preferencias no racionales o factores externos, lo que complica aún más el análisis teórico.
Investigaciones actuales
Las investigaciones contemporáneas continúan explorando el ámbito del equilibrio de Nash y sus aplicaciones. Por ejemplo, se han realizado estudios para integrar la inteligencia artificial y el aprendizaje automático en los modelos de teoría de juegos, buscando nuevas maneras de entender la cooperación en redes complejas. Estos trabajos están comenzando a desentrañar cómo las tecnologías emergentes pueden modelar comportamientos económicos y sociales de maneras novedosas.
Tendencias relacionadas
Además, el análisis del comportamiento humano en plataformas digitales y redes sociales está transformando las maneras en que se aplica el equilibrio de Nash. La manera en que los usuarios toman decisiones en línea, comparten información y forman comunidades puede verse iluminada a través del prisma de la teoría de juegos. Así, las interacciones en una plataforma pueden modelarse como un juego en el que el equilibrio de Nash podría ayudar a predecir comportamientos colectivos, promoviendo una mejor comprensión de las dinámicas sociales contemporáneas.
En una era de interconexión global, el equilibrio de Nash se perfila como un concepto crucial para comprender cómo interactuamos y tomamos decisiones en presencia de otros. Su aplicación va mucho más allá del ámbito académico, tocando aspectos cotidianos de la vida, desde la competencia en el mercado hasta la colaboración en equipos de trabajo. La teoría continúa desarrollándose, impulsada por las tecnologías emergentes y la necesidad de comprender conductas humanas en un mundo cada vez más complejo.