La cotangente es una de las funciones trigonométricas fundamentales que se puede definir como el cociente entre el coseno y el seno. En términos matemáticos, se expresa como:
cot(x) = cos(x) / sin(x)
Esta función es clave en la resolución de múltiples problemas en diversas áreas, incluyendo la física, la ingeniería y las matemáticas puras.
Derivación de la Cotangente
Fórmula de Derivada de la Cotangente
La derivada de la cotangente se puede calcular utilizando las reglas básicas de la derivación. La fórmula estándar para la derivada de la cotangente es:
d/dx[ cot(x) ] = -cosec²(x)
Demostración de la Derivada
Para encontrar la derivada de cot(x), se utiliza la regla del cociente. Aplicando la derivada a la definición de cotangente:
cot(x) = cos(x) / sin(x)
Usando la regla del cociente:
f'(x) = (g(x)h'(x) – h(x)g'(x)) / (h(x))²
En este contexto:
- g(x) = cos(x)
- h(x) = sin(x)
- g'(x) = -sin(x)
- h'(x) = cos(x)
Al aplicar la regla del cociente, obtenemos:
d/dx[ cot(x) ] = (sin(x)(-sin(x)) – cos(x)cos(x)) / sin²(x)
Esto se simplifica a:
– (sin²(x) + cos²(x)) / sin²(x)
Utilizando la identidad sin²(x) + cos²(x) = 1, llegamos a:
d/dx[ cot(x) ] = -1 / sin²(x)
Y recordando que cosecante es la inversa del seno, se escribe como:
d/dx[ cot(x) ] = -cosec²(x)
Aplicaciones de la Derivada de Cotangente
Uso en Cálculo de Máximos y Mínimos
Una de las aplicaciones más comunes de la derivada de cotangente es en el cálculo de máximos y mínimos de funciones. Cuando se busca optimizar funciones, es fundamental encontrar los puntos críticos, que se obtienen igualando la derivada a cero:
-cosec²(x) = 0
Sin embargo, como la cosecante nunca es cero, eso indica que la cotangente no tiene máximos ni mínimos, lo que es significativo en el análisis de funciones.
Estudio de la Concavidad
La segunda derivada también es crucial en la comprensión de la concavidad de la función cotangente. Calculando la segunda derivada:
d²/dx²[ cot(x) ] = d/dx[-cosec²(x)]
Aplicando la derivada:
d²/dx²[ cot(x) ] = -2cot(x)cosec²(x)
El signo de esta derivada determinará si la función es cóncava hacia arriba o hacia abajo, lo que puede ser crucial en diversas aplicaciones de modelado.
Problemas de Física
En física, la cotangente y su derivada son herramientas útiles para entender fenómenos relacionados con ángulos y vibraciones. Por ejemplo, al estudiar ondas, la cotangente puede ser utilizada para describir ciertas oscilaciones, y su derivada nos ayuda a entender la tasa de cambio en la amplitud de esas oscilaciones.
Ejemplos Prácticos
Ejemplo 1: Cálculo de Derivadas
Sea f(x) = cot(x). Calculemos su derivada:
f'(x) = -cosec²(x)
Este resultado significa que la derivada de la cotangente es siempre negativa, lo que implica que la función cotangente está decreciendo en su dominio.
Ejemplo 2: Optimización en Contexto Real
Supongamos que estamos diseñando un puente y necesitamos calcular el ángulo óptimo para minimizar el uso de materiales. Usando cotangentes podemos modelar el problema y emplear la derivada para encontrar el ángulo que minimiza la resistencia.
Ejemplo 3: Movimiento de Proyectiles
En física, al estudiar el movimiento de proyectiles, las funciones trigonométricas son esenciales. El ángulo de lanzamiento puede describirse con la función cotangente, y su derivada puede ayudarnos a determinar el instante en que el proyectil alcanza su altura máxima.
Gráficas de la Cotangente
Comportamiento General
La gráfica de la función cotangente presenta un comportamiento particular. Los valores de cot(x) son indefinidos en los puntos donde sin(x) = 0 (números enteros de π). Así, la gráfica tendrá asíntotas verticales en esos puntos, alternando entre valores positivos y negativos.
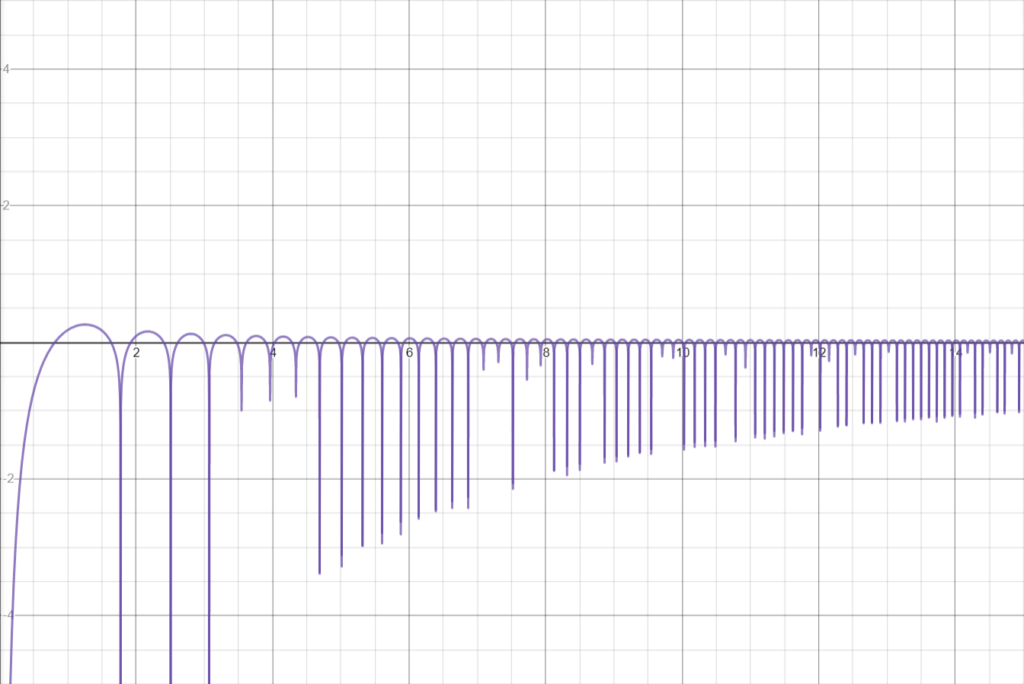
Interpretación Visual de la Derivada
El gráfico de la derivada -cosec²(x) permite visualizar cómo la cotangente decrece continuamente sin alcanzar un mínimo plano. La persistente negatividad de la derivada resalta el comportamiento decreciente de la función.
Relación con Otras Funciones Trigonométricas
Comparación con Tangente y Cotangente
La función cotangente se relaciona directamente con la tangente. Su derivada muestra que, a medida que la cotangente disminuye, la tangente, que es su inversa, aumenta, demostrando la interdependencia entre estas funciones.
Aplicaciones en Cálculo Integral
Además de derivadas, las funciones cotangente tienen aplicaciones en integrales. Conociendo su derivada, podemos identificar que el integral de cosecante al cuadrado es también fundamental en cálculos de área bajo curvas, especialmente en trigonometría.
El estudio de la derivada de la cotangente es esencial para profundizar en el entendimiento de las funciones trigonométricas y su aplicación en problemas reales. Desde la optimización en ingeniería hasta el análisis de fenómenos físicos, la cotangente y sus propiedades son herramientas invaluables en el mundo matemático y sus disciplinas afiliadas.